SISTEMA GRACELI TRANSSIMÉTRICO QUÂNTICO E TOPOLÓGICO.

O SISTEMA GRACELI TRANSSIMÉTRICO E TRANSRENORMALIZÁVEL DEFINE QUE UMA OU QUALQUER TIPO DE PARTÍCULA OU FENÔMENO EM GERAL SE ENCONTRA EM TRANSSIMETRIA E TRANSRENORMALIZAÇÃO..

OU SEJA , ENTRA E SAI DE SIMETRIA E RENORMALIZAÇÃO EM TERMOS DE INFINITÉSIMOS, ONDE UMA PARTE AUMENTA A SUA ENERGIA E ESTADOS QUÂNTICO E TOPOLÍGOCO [OU MESMO DIMENSÕES E ESTADOS QUÂNTICOS DE GRACELI [VER NA INTERNET], E OUTROS DIMENUEM, NISTO TEM UM PONTO CRÍTICO DE VALOR ENTRE AS PASSAGENS DE UM AUMENTO PARA UM DECRÉSCIMO, EM TERMOS INFINITÉSIMOS EM RELÇÃO AO TEMPO, POENCIAL EINTENSIDADE DE ENERGIAS, E OUTROS.

MECÃNICA GRACELI GERAL - QTDRC.

$equação Graceli dimensional relativista tensorial quântica de campos$

$\psi ^{*}$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

[

$\psi ^{*}$

$TeoriaInteraçãomediadorMagnitude relativaComportamentoFaixaCromodinâmicaForça nuclear forteGlúon10411/r71,4 × 10-15 mEletrodinâmicaForça eletromagnéticaFóton10391/r2infinitoFlavordinâmicaForça nuclear fracaBósons W e Z10291/r5 até 1/r710-18 mGeometrodinâmicaForça gravitacionalgráviton101/r2infinito$

Teoria	Interação	mediador	Magnitude relativa	Comportamento	Faixa
Cromodinâmica	Força nuclear forte	Glúon	1041	1/r7	1,4 × 10-15 m
Eletrodinâmica	Força eletromagnética	Fóton	1039	1/r2	infinito
Flavordinâmica	Força nuclear fraca	Bósons W e Z	1029	1/r5 até 1/r7	10-18 m
Geometrodinâmica	Força gravitacional	gráviton	10	1/r2	infinito

$G* = OPERADOR DE DIMENSÕES DE GRACELI.$

DIMENSÕES DE GRACELI SÃO TODA FORMA DE TENSORES, ESTRUTURAS, ENERGIAS, ACOPLAMENTOS, , INTERAÇÕES E CAMPOS, DISTRIBUIÇÕES ELETRÔNICAS, ESTADOS FÍSICOS, ESTADOS QUÂNTICOS, ESTADOS FÍSICOS DE ENERGIAS DE GRACELI, E OUTROS.

/ $\psi ^{*}$ [ $\psi ^{*}$ ${\boldsymbol {\mu }}$ ] $\lambda$ ω ${\mathcal {T}}$ , $\sigma$ , $\psi$ $F^{\mu \nu }$ $T^{\mu \nu }$ $P^{\mu }\!$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$

(1)\qquad {\mathcal {L}}=\partial ^{\mu }\phi \partial _{\mu }\phi -V(\phi ).

\left|\psi \right\rangle ={\frac {1}{\sqrt {2}}}{\bigg (}\left|\uparrow \downarrow \right\rangle -\left|\downarrow \uparrow \right\rangle {\bigg )},

/ $\psi ^{*}$ [ $\psi ^{*}$ ${\boldsymbol {\mu }}$ ]

\lambda

{\mathcal {T}}

\sigma

\psi

F^{\mu \nu }

T^{\mu \nu }

P^{\mu }\!

-i\hbar {\frac {\partial }{\partial x_{n}}}

.

\left|\psi ({\vec {r}},t)\right\rangle

(2)\qquad V(\phi )=-10|\phi |^{2}+|\phi |^{4}\,

{+, - ] / EV/

\left|\psi \right\rangle ={\frac {1}{\sqrt {2}}}{\bigg (}\left|\uparrow \downarrow \right\rangle -\left|\downarrow \uparrow \right\rangle {\bigg )},

/ $\psi ^{*}$ [ $\psi ^{*}$ ${\boldsymbol {\mu }}$ ]

\lambda

{\mathcal {T}}

\sigma

\psi

F^{\mu \nu }

T^{\mu \nu }

P^{\mu }\!

-i\hbar {\frac {\partial }{\partial x_{n}}}

.

\left|\psi ({\vec {r}},t)\right\rangle

(3)\qquad \phi ={\sqrt {5}}e^{i\theta }

{+, - ] / EV/

\left|\psi \right\rangle ={\frac {1}{\sqrt {2}}}{\bigg (}\left|\uparrow \downarrow \right\rangle -\left|\downarrow \uparrow \right\rangle {\bigg )},

/ $\psi ^{*}$ [ $\psi ^{*}$ ${\boldsymbol {\mu }}$ ]

\lambda

{\mathcal {T}}

\sigma

\psi

F^{\mu \nu }

T^{\mu \nu }

P^{\mu }\!

-i\hbar {\frac {\partial }{\partial x_{n}}}

.

\left|\psi ({\vec {r}},t)\right\rangle

{\mathcal {L}}={\bar {\psi }}_{B}\left[i\gamma _{\mu }\left(\partial ^{\mu }+ie_{B}A_{B}^{\mu }\right)-m_{B}\right]\psi _{B}-{\frac {1}{4}}F_{B\mu \nu }F_{B}^{\mu \nu }

Quebra espontânea de simetria é um processo pelo qual um sistema simétrico passa, de forma espontânea, para um estado não simétrico. Este tipo de processo, incomum na natureza física, é vital para a compreensão do modelo padrão das partículas fundamentais, que é um dos mais importantes ramos da física moderna.

Definição[editar | editar código-fonte]

Para que uma quebra espontânea de simetria ocorra, deve necessariamente haver um sistema no qual existam diversos estados subsequentes com iguais probabilidades de ocorrer. Este sistema, como um todo, então é tratado como um sistema simétrico. Entretanto apenas um dos estados subsequentes deve ocorrer e toda a probabilidade dos inúmeros estados diversos é reduzida a zero, já que não há mais simetria. Então, é dito que a simetria do sistema foi espontaneamente quebrada.

Definição formal[editar | editar código-fonte]

Quando uma teoria é dita simétrica com respeito à um grupo simétrico, mas afirma que um elemento deste grupo é distinto, então uma quebra espontânea de simetria ocorreu, ou seja, pela teoria, não é necessário que se identifique o elemento e sim apenas que haja um elemento distinto.

Importância no modelo padrão[editar | editar código-fonte]

Ver artigo principal: Mecanismo de Higgs

Sem a quebra espontânea de simetria o modelo padrão prediz a existência de um determinado número de partículas. Entretanto, algumas destas partículas (os bosões W e Z, por exemplo) são preditos de não possuir massa, quando na realidade eles possuem massa. Esta era a maior falha do modelo até que o físico escocês Peter Higgs e outros propuseram, através do que ficou conhecido por mecanismo de Higgs, o uso da quebra espontânea de simetria para comportar massa nestas partículas. O mecanismo por sua vez prediz a existência de uma nova partícula, o bosão de Higgs. O bosão/bóson de Higgs foi detectado no LHC do CERN em Julho de 2012, com probabilidade maior que 5 sigmas de ser verdadeira tal identificação.

Uso na matemática[editar | editar código-fonte]

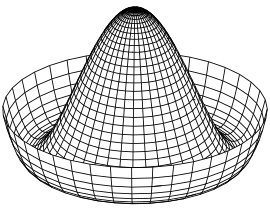
Na matemática o uso mais comum da quebra espontânea de simetria é pelo uso da Função de Lagrange, a qual essencialmente indica como um sistema irá se comportar por meio de termos potenciais

(1)\qquad {\mathcal {L}}=\partial ^{\mu }\phi \partial _{\mu }\phi -V(\phi ).

É neste termo potencial $V(\phi )$ que a ação da quebra de simetria ocorre. Como demonstra o gráfico do chapéu mexicano

(2)\qquad V(\phi )=-10|\phi |^{2}+|\phi |^{4}\,

Este termo potencial possui vários possíveis mínimos dados por

(3)\qquad \phi ={\sqrt {5}}e^{i\theta }

para qualquer real no intervalo $0<\theta <2\pi$ . Este sistema também possui um estado do vácuo quântico que corresponde ao $\phi =0$ , este estado possui um grupo unitário simétrico. Entretanto, uma vez que o sistema atinja um estado específico no vácuo (que corresponda a um valor para $\theta$ ) a simetria será espontaneamente quebrada.

A renormalização é um conjunto de técnicas utilizadas para eliminar os infinitos que aparecem em alguns cálculos em Teoria Quântica de Campos.^[1] Na mecânica estatística dos campos^[2] e na teoria de estruturas geométricas auto-similares,^[3] a renormalização é usada para lidar com os infinitos que surgem nas quantidades calculadas, alterando valores dessas quantidades para compensar os efeitos das suas auto-interações. Inicialmente vista como um procedimento suspeito e provisório por alguns de seus criadores, a renormalização foi posteriormente considerada uma ferramenta importante e auto-consistente em vários campos da física e da matemática. A renormalização é distinta da outra técnica para controlar os infinitos, regularização, que assume a existência de uma nova física desconhecida em novas escalas.^[4]

Renormalização em EDQ[editar | editar código-fonte]

Em Lagrangeano de EDQ,

{\mathcal {L}}={\bar {\psi }}_{B}\left[i\gamma _{\mu }\left(\partial ^{\mu }+ie_{B}A_{B}^{\mu }\right)-m_{B}\right]\psi _{B}-{\frac {1}{4}}F_{B\mu \nu }F_{B}^{\mu \nu }

Os campos e a constante de acoplamento são realmente quantidades "cruas", por isso, o índice $B$ acima. Convencionalmente, as quantidades cruas são escritas de modo que os termos lagrangianos correspondentes sejam múltiplos dos renormalizados:

\left({\bar {\psi }}m\psi \right)_{B}=Z_{0}{\bar {\psi }}m\psi

\left({\bar {\psi }}\left(\partial ^{\mu }+ieA^{\mu }\right)\psi \right)_{B}=Z_{1}{\bar {\psi }}\left(\partial ^{\mu }+ieA^{\mu }\right)\psi

\left(F_{\mu \nu }F^{\mu \nu }\right)_{B}=Z_{3}\,F_{\mu \nu }F^{\mu \nu }.

Teoria de gauge e Identidade de Ward-Takahashi^[5]^[6] implicam que podemos renormalizar os dois termos da parte derivada covariante ${\bar {\psi }}(\partial +ieA)\psi$ juntos^[7], que é o que aconteceu para $Z 2$ , é o mesmo com $Z 1$ .^[8]

Pesquisar este blog

SISTEMA GRACELI TRANSSIMÉTRICO QUÂNTICO E TOPOLÓGICO.

Definição[editar | editar código-fonte]

Definição formal[editar | editar código-fonte]

Importância no modelo padrão[editar | editar código-fonte]

Uso na matemática[editar | editar código-fonte]

Renormalização em EDQ[editar | editar código-fonte]

Comentários

Postar um comentário

Postagens mais visitadas deste blog